[NLP] Neural Network
Neural Network
이번 포스팅에서는 딥러닝의 기초, Neural Network (NN) 에 대해서 알아보는 시간을 갖도록 하겠다. NN은 input을 받아 여러 neuron들로 이루어진 hidden layers를 거쳐 output을 뱉어내는 구조를 가지고 있는데, 사람의 neuron에서 따와 Neural network라는 이름이 붙었다. Hidden layers를 몇 개로 할지, loss는 무엇으로 둘 지, 각종 파라미터 및 output은 어떻게 결정할 지 등등에 따라 각기 다른 모델이 나오게 된다. 이제부터 NN의 구조 및 디테일에 대해 알아보자.
Basic Architecture
Neural Network 는 기본적으로 아래와 같은 모양을 하고 있다.
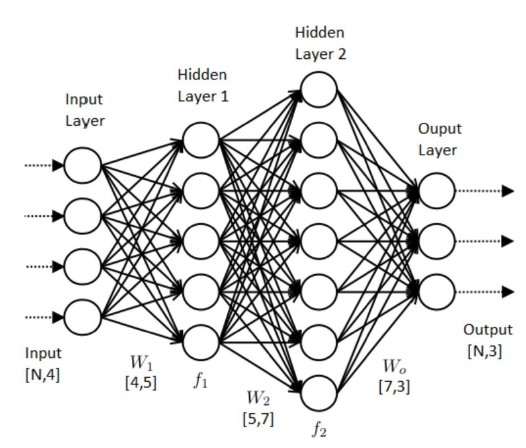
단순한 Prediction task의 경우 output으로 예측값 자체를 나오게 할 수 있고, Classification 과 같은 task에서는 output으로 predicted probability를 나오게 하여 활용할 수도 있다.
NN에서는 각 hidden layer마다 상응하는 weight matrix (및 bias term)를 두어 곱해가며 Forward 시켜주고, 정의된 loss function 을 이용해 Backpropagation 하여 보다 정확한 Output이 나오도록 하는 구조를 가지고 있다. 이 과정에서 쓰이는 hidden layers의 개수, learning rate 설정, input 및 output 노드의 수 등은 사용자가 선택할 수 있다.
그렇다면 이제 Loss의 종류, Training 방법, Feed-forward 및 Backpropagation 등에 대해 더 살펴보도록 하자.
Loss
수행하고자 하는 Task가 무엇인지에 따라 다양한 loss function을 선택해줄 수 있지만, 일반적으로 MSE (Mean Squared Error)나 Cross-Entropy를 많이 사용한다. 보통 MSE는 numeric한 prediction 등에 주로 사용되고, Cross-Entropy는 classification과 같은 task에 주로 활용된다. 물론 사용자가 특별히 customize한 loss function을 사용하는 것도 가능하나, 미분 가능성 등을 고려해주어야 한다.
Loss function을 잘 정의해주어야 NN training 시 파라미터 업데이트가 보다 정교하게 되어 모델의 정확도를 높일 수 있으니 신중히 결정해주도록 하자.
-
MSE :
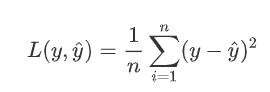
-
Cross-Entropy :
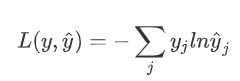
Training
NN을 훈련시키기 위해서는 다음의 과정을 거친다.
- 1) Input 입력
- 2) Initialize Parameters (보통 randomly assign)
- 3) Hidden layers를 거쳐 Loss 계산
- 4) 계산된 Loss를 바탕으로 gradient를 구하고 주로 Gradient descent를 통해 backpropagate
- 5) Update parameters
- 6) 사전에 정해준 epoch 수만큼 or Stop criterion 충족 시까지 반복
Gradient Descent (GD)는 Loss function을 업데이트 대상이 되는 파라미터들로 각각 편미분하여 나온 값(gradient)에 learning rate를 곱한 값만큼 기존 파라미터에서 빼주어 최적값에 도달할 수 있도록 업데이트 해나가는 방법이다. 따라서 이 방법을 쓸 때는 일반적으로 loss function이 미분 가능한 지 등을 체크해주어야 한다. GD에는 Stochastic GD, Mini-batch GD 등 업데이트를 batch 단위로 나눠서 할 것인지 등을 기준으로 하는 여러 방법이 존재한다.
이 때, Hidden layers를 거쳐 값이 나오는 것을 Forward propagation 이라고 하고, GD 등을 통해 파라미터를 업데이트 해주는 과정을 Back-propagation 이라고 한다. Forward를 해줄 때는 단순한 linear combination에서 벗어나 좀 더 복잡한 형태를 학습할 수 있도록 하기 위해 중간중간 non-linear activation function을 섞어주며, 그 종류에는 ReLU, Sigmoid, tanh, Elu 등등이 있다.
지금까지 NN의 기본 구조 및 구성 요소, 훈련 방법에 대해 알아보았다. 코드를 통해 알고리즘을 구현해보면 더 이해하기 쉽다. 아래는 직접 구현한 Basic NN의 python code 이다.
## Import necessary packages (ONLY numpy & matplotlib)
import numpy as np ## Import Numpy as the name 'np'
import matplotlib.pyplot as plt ## Import matplotlib as 'plt'
## Import data for Neural Network
data = np.loadtxt('training.txt') ## Load file (Assume data & code files are in the same folder)
np.random.shuffle(data) ## Randomly shuffle the data for training
## Uncomment the line below to check the data shape
#print(data.shape) ## (1000,3)
## Split X(feature) & Y(label)
x = data[:,:-1] ## Save features as variable 'x'
t = data[:,-1] ## Save labels as variable 't'
## Set parameters
K = 2 ## input layer size = 2
N = 8 ## hidden layer size = 8
M = 1 ## output layer size = 1
lr = 0.01 ## learning rate = 0.01
## Make kind of placeholders for upcoming variables
y = np.zeros((1000,M)) ## Create zero vector to initialize predicted outputs
t_label = t.reshape(-1,M) ## Reshape the true labels and save it <- (1000,1)
## Initialize Weights
w = np.random.random((K,N)) ## Initialize Weight for input -> hidden
wp = np.random.random((N,M)) ## Initialize Weight for hidden -> output
## Define activation function (-> sigmoid)
def sigmoid(x): ## Define the function named 'sigmoid'
return 1/(1+np.exp(-x)) ## sigmoid(x) = 1 divided by (1+exp(-x))
## Training
epochs = 50 ## Set the number of epochs (50 here)
## Below Variable is for plotting
loss_avg = []
for epoch in range(epochs): ## Repeat for 'epochs'(=50 here) times
losses = np.zeros(len(x)) ## Create zero vector for loss
for iter in range(len(x)): ## Repeat for len(x)(=1000) times (SGD)
## Forward pass
## Initialize u(sum of w*x) & h(hidden state)
u = np.zeros(N) ## Zero vector for u (input -> hidden)
up = np.zeros(M) ## Zero vector for up (hidden -> output)
h = np.zeros(N) ## Zero vector for hidden state (=sigmoid(u))
## Input -> Hidden direction
for i in range(N): ## Repeat for N times (col for input->hidden)
for k in range(K): ## Repeat for K times (row for input->hidden)
u[i] = u[i] + w[k,i]*x[iter,k] ## Scalar form for u = sum(w*x)
h[i] = sigmoid(u[i]) ## Scalar form for h=sigmoid(u)
## Hidden -> Output direction
for j in range(M): ## Repeat for M times (col for hidden->output)
for i in range(N): ## Repeat for N times (row for hidden->output)
up[j] = up[j] + wp[i,j]*h[i] ## Scalar form for up = sum(wp*h)
y[iter,j] = sigmoid(up[j]) ## Scalar form for y=sigmoid(up)
## BackPropagation
## Variables for gradients
EI = np.zeros(N) ## Zero vector for EI (Hidden -> Input)
EIP = np.zeros(M) ## Zero vector for EIP (Output -> Hidden)
## Output -> Hidden direction (Reverse order of Forward pass)
for j in range(M): ## Repeat for M times (Output layer size)
## Compute gradient for output->hidden (=(pred-true)*y*(1-y))
EIP[j] = (y[iter,j]-t_label[iter,j]) * y[iter,j] * (1-y[iter,j])
## Hidden -> Input direction
for i in range(N): ## Repeat for N times
for j in range(M): ## Repeat for M times
## Compute gradient for hidden->input (=sum(EIP*wp*h*(1-h)))
EI[i] = EI[i] + EIP[j]*wp[i,j]*h[i]*(1-h[i])
## Update weights
## Weight for hidden -> output
for i in range(N): ## Repeat for N times
for j in range(M): ## Repeat for M times
## Scalar form of updating eq. (wp = wp-lr*EIP*h)
wp[i,j] = wp[i,j] - lr*EIP[j]*h[i]
## Weight for input -> hidden
for k in range(K): ## Repeat for K times
for i in range(N): ## Repeat for N times
## Scalar form of updating eq. (w = w-lr*EI*x)
w[k,i] = w[k,i] - lr*EI[i]*x[iter,k]
## Loss
for i in range(M): ## Repeat for M times
## Scalar form for MSE loss (= 0.5*(pred-true)^2)
losses[iter] = losses[iter] + (0.5*(y[iter,i]-t_label[iter,i])**2)
loss_avg.append(np.mean(losses)) ## Calculate average of loss
## Plotting
epoch_lst = list(range(epochs)) ## Create list of epochs for x-axis
## Plot x:As epoch proceeds -> y:Total loss changes (point marker='o')
plt.plot(epoch_lst, loss_avg, marker='o')
plt.show() ## Show the plot
이번 포스팅에서는 NN에 대한 설명과 구현 코드까지 모두 살펴보았다. 딥러닝의 가장 기초가 되는 부분이므로 한 번 공부할 때 정확히, 잘 이해하고 넘어가도록 하자.